09月
22

python实现牛顿法迭代法

发表于

最近看到牛顿迭代法和二分法，现在用python实现一下

拿开方举例,转载自Python编程实现二分法和牛顿迭代法求平方根代码

一、使用二分法实现开方

假设求根号5，二分法的基本思路是

1
2
3
4
5
6
a:折半： 5/2=2.5
b:平方校验: 2.5*2.5=6.25>5，并且得到当前上限2.5
c:再次向下折半:2.5/2=1.25
d:平方校验：1.25*1.25=1.5625<5,得到当前下限1.25
e:再次折半:2.5-(2.5-1.25)/2=1.875
f:平方校验：1.875*1.875=3.515625<5,得到当前下限1.875

每次得到当前值和5进行比较，并且记下下下限和上限，依次迭代，逐渐逼近平方根：

  • 当结果校验超过原值，继续迭代
  • 当结构校验低于原值，获得另一半，继续迭代

python代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import math
from math import sqrt

def sqrt_binary(num):
    x = sqrt(num)
    y = num/2.0
    low = 0.0
    up = num*1.0
    count = 1
    while abs(y-x)>0.000001:
        print(count,y)
        count += 1
        if y*y>num :
            up = y
            y = low+(y-low)/2
        else:
            low = y
            y = up-(up-y)/2
    return y

二、使用牛顿迭代法实现开方

从函数意义上理解：我们是要求函数f(x)=x²，使f(x)=num的近似解，即x²-num=0的近似解。

从几何意义上理解：我们是要求抛物线g(x)=x²-num与x轴交点（g(x)=0）最接近的点。

我们假设g(x0)=0，即x0是正解，那么我们要做的就是让近似解x不断逼近x0，这是函数导数的定义：

可以由此得到

img

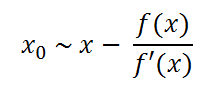
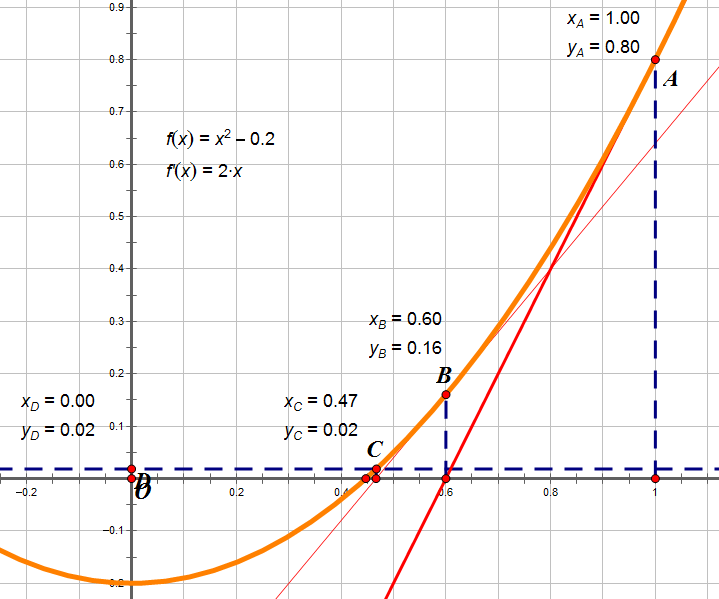
从几何图形上看，因为导数是切线，通过不断迭代，导数与x轴的交点会不断逼近x0。

对于一般情况：

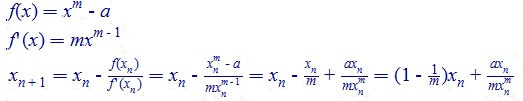
将m=2代入：

1
2
3
4
5
6
7
8
9
10
11
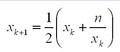
12
def sqrt_newton(num): 
  x=sqrt(num) 
  y=num/2.0 
  count=1 
  while abs(y-x)>0.00000001: 
    print count,y 
    count+=1 
    y=((y*1.0)+(1.0*num)/y)/2.0000 
  return y 
 
print(sqrt_newton(5)) 
print(sqrt(5))

三、利用牛顿迭代法实现立方

1
2
3
4
5
6
7
8
9
10
11
12
def cube_newton(num): 
  x=num/3.0 
  y=0 
  count=1 
  while abs(x-y)>0.00000001: 
    print count,x 
    count+=1 
    y=x 
    x=(2.0/3.0)*x+(num*1.0)/(x*x*3.0) 
  return x 
 
print(cube_newton(27))
分享到：